링크
Lecture 3: String Manipulation, Guess and Check, Approximations, Bisection | Introduction to Computer Science and Programming in
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Review / Preview
저번 시간 내용 : https://ikablog.tistory.com/5
1. 문자열 (String)
2. 제어 흐름 - if, elif, else
3. 반복문 - while, for
---
이번 시간 내용 :
1. 문자열 가지고 놀기, string manipulation
len(), indexing, sclicing, 문자열 iteration
2. 몇 가지 알고리즘들
guess and check algorithm
근사 (approximate solutions)
이분법 (bisection method)
1. String manipulation
문자열에 쓸 수 있는 몇 가지 유용한 함수들.
1. len() : 문자열의 길이를 반환.
len("Hello!") #6. H, e, l, l, o, ! 의 여섯 가지 문자로 되어있으므로 6이 나온다.
2. 문자열[n] : 문자열에서 n의 index를 가진 문자를 반환한다.
index는 0부터 세기 시작한다!! 첫 번째 문자는 0, 두 번째 문자는 1... 이런 식으로 나간다.
즉, s[0]은 s 문자열의 첫 번째 문자를 반환하고, s[1]은 s 문자열의 두 번째 문자를 반환하고...
n번째 글자를 따오고 싶다면 s[n-1]을 입력해야 한다.
음수의 index도 가능하다. 이때는 끝에서부터 센다.
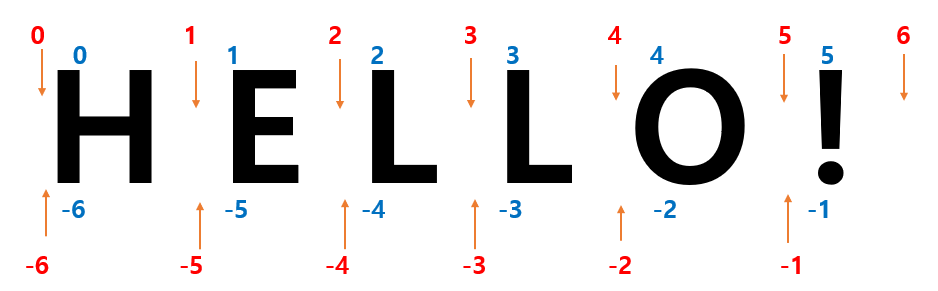
s = abc
s[0] # 'a' 가 나온다. 0부터 세기 시작!
s[1] # 'b' 가 나온다.
s[2] # 'c' 가 나온다.
s[-1] # 'c' 가 나온다. 끝에서 첫 번째 문자.
s[-3] # 'c' 가 나온다. 끝에서 세 번째 문자.
s[3] # 에러가 뜬다. 네 번째 문자는 없기 때문.
문자열[start:stop] : 문자열에서 start부터 stop번째 index 사이를 떼어온다.
s[0:1]을 하면 s[0]만 떨어져나오고, s[0:5]를 하면 첫 번째 문자부터 다섯 번째 문자까지 떼어져 나온다.
여기서도 음수의 index를 쓸 수 있다. s[0:-1]을 하게 되면 마지막 글자만 빠지게 된다.
slicing에서 start값을 비워두면 기본값으로 0이 적용되고, stop 값을 비워두면 기본값으로 해당 문자열의 len()이 적용된다.
s = "abcdef"
s[1:4] #bcd
s[3:5] #de
s[3:-1] #de
s[0:3] #abc
s[:3] #start의 기본값으로 0이 적용되어서 똑같이 abc가 나온다.
s[3:len(s)] #def , len(s) = 6. 간단하게 len(s)가 마지막 인덱스라고 생각하면 된다.
s[3:] #stop의 기본값으로 len(s)가 적용되어서 똑같이 def가 나온다.
s[0:0] # 빈 문자열
slicing에 step을 추가할 수 있다. 즉, 문자열[start:stop:step]의 방식으로 사용이 가능하다.
step을 추가하면 step의 간격으로 문자열을 추출하게 된다.
step에 음수를 쓸 수도 있다. 음수를 쓰면 문자를 역순으로 배열하게 된다.
step을 생략하면 기본값은 1이 되고, 그게 [start:stop]이다.
s = 'abcdefgh'
s[1:8:2] #bdfh
s[1:8:3] #beh
s[1:8:-1] #빈 문자열이 나온다.
s[8:1:-1] #이렇게 해야 hgfedc가 나온다. 역순이니까 뒤에서 시작해서 앞으로 가야한다.
s[::2] #aceg. 비워놓기는 여전히 유효하다.
s[3::-1] #dcba. step에 음수를 적어두면 start의 기본값이 len(s)가 되고 stop의 기본값이 0이 된다.
s[::-1] #hgfedcba. 문자열 뒤집기
늘 그렇지만 직접 가지고 놀면서 감을 잡는 게 제일 중요하다.
한편, string은 indexing으로 바꿀 수 없다. string을 바꾸고 싶다면 아예 새로 할당을 해줘야 한다.
s = "Hat is yellow."
s[0] = 'C' #오류가 난다.
s = 'C' + s[1:] #이런식으로 아예 새로 할당을 해줘야 한다.
String은 iterable한 객체이다. for loop에 쓸 수 있다.
s = input("단어를 입력해주세요.")
for c in s :
if c == 'a' :
print ("단어에 a가 있습니다.")
break
물론 range()와 indexing을 사용해서 이런 코드를 짤 수도 있다.
s = input("단어를 입력해주세요.")
for i in range(len(s)) :
if s[i] == 'a' :
print (str(i+1)+"번째 글자에 a가 있습니다.")
여기서부터는 응용에 대한 내용.
지금까지 배운 함수로 이것저것 뽁작뽁작해보는 시간.
2. Guess and Check method
어떠한 수를 받았을 때 세제곱근을 구하는 프로그램을 짜보자.
세 제곱근이 자연수가 아니라면 (ex>5) "자연수의 세 제곱이 아니에요." 를 출력하고,
세 제곱근이 자연수라면 (ex>8) "세 제곱근은 ~~~입니다" 를 출력한다.
물론 프로그래밍에 정답은 없다. 모로 가도 서울로만 가면 된다.
일단 이번 시간에는 Guess and check method를 이용한 방법을 소개한다.
Guess and Check method : 일단 넣어보고, 맞으면 앗싸, 틀리면 아쉽다 하는 방법.
먼저 1의 세 제곱을 해본다. 입력한 수와 일치하면 "세 제곱근은 1입니다."를 출력, 틀리면 다음으로.
그 다음 2의 세 제곱을 해본다. 입력한 수와 일치하면 "세 제곱근은 2입니다."를 출력, 틀리면 다음으로.
이런 식으로 쭉쭉쭉 해보다가, 세 제곱이 입력한 수보다 크면 더 해볼 필요가 없어지니, 이때 "자연수의 세 제곱이 아니에요" 를 출력하면 된다. 이 뒤로는 훨씬 커질테니까.
cube = int(input ("숫자를 입력해주세요."))
for guess in range(cube+1) :
if guess ** 3 == cube :
print ("세 제곱근은",guess,"입니다.")
break
if guess ** 3 > cube :
print("자연수의 세 제곱이 아니에요.")
break
3. 근사하기 (Approximation)
어떠한 수를 받았을 때 세제곱근의 근사치를 구하는 프로그램을 짜보자.
출력값의 세제곱은 입력값과 0.01 이내의 차이를 보여야 한다.
Guess and check의 심화 버전.
"근사한 답을 찾고 싶을 때", 조금씩 조금씩 값을 바꿔보면서 오차를 줄인다. 그렇게 정답과 "충분히 가까운" 값을 찾아내면 된다. ( |계산한 값 - 실제 값| < ε 일 때의 값을 찾는 것.)
값을 바꾸는 정도가 커질수록 오차가 커진다. 대신 계산량은 줄어든다.
반대로 값을 바꾸는 정도가 작아질수록 오차가 작아지고, 계산량은 늘어난다.
일단 0.0001 단위로 값을 바꾸는 프로그램을 짜보자.
0부터 시작한다. 만약 |계산한 값 - 실제 값| < 0.01이 라면 해당 숫자를 출력하고 프로그램을 종료한다.
그 다음 0.0001으로도 해보고, 0.0002로도 똑같이 해본다. 그렇게 쭉쭉쭉 해본다.
만약 세 제곱이 입력한 수보다 커졌는데도 |계산한 값 - 실제 값| < 0.01 인 값이 안나왔다면, 0.0001 단위에선 오차를 충분히 좁힐 수 없는 것이다. 세제곱근을 구하지 못했다고 출력하면 된다.
cube = int(input ("숫자를 입력해주세요."))
epsilon = 0.01 #허용 오차
guess = 0 #예측값
increment = 0.0001 #1회 증가량
num_guess = 0 #예측횟수
while abs(guess**3-cube) >= epsilon : #abs()는 절댓값을 반환하는 함수이다.
guess += increment # a += b는 a = a+b 와 똑같은 표현이다.
num_guess += 1
if (guess**3 > cube) :
break #아까와 마찬가지로, 여기서부턴 더 해봤자 오차가 커지기만 함.
if abs(guess**3-cube) < epsilon :
print ("세 제곱근은",guess,"입니다. 총",num_guess,"회 예측하였습니다.")
else :
print (epsilon,"이내의 오차를 가지는 세제곱근을 구하지 못했습니다.")
가지고 놀다보면, epsilon이 작아질수록 세 제곱근을 구하지 못하는 경우가 왕왕 많아진다는 걸 알 수 있다. 그럴 땐 increment를 줄이면 된다. 자연스럽게 예측 횟수는 엄청나게 뻥튀기된다. 예측하기는 항상 이런 식이다. 더 정확한 값을 구하고 싶다면 더 많이 계산해야 하고, 속도를 중시한다면 정확도는 타협해야 한다. (물론 더 나은 알고리즘을 쓴다는 방법도 있지만...)
4. Bisection method
A와 B가 게임을 한다.
A는 1부터 1000까지 숫자를 하나 고른다. B는 그 숫자를 맞춰야 한다.
B가 숫자를 고를 때마다, 그 숫자가 A가 고른 숫자보다 더 큰지 작은지를 알려준다.
이때 B는 항상 10번 이내에 A가 고른 숫자를 맞출 수 있다.
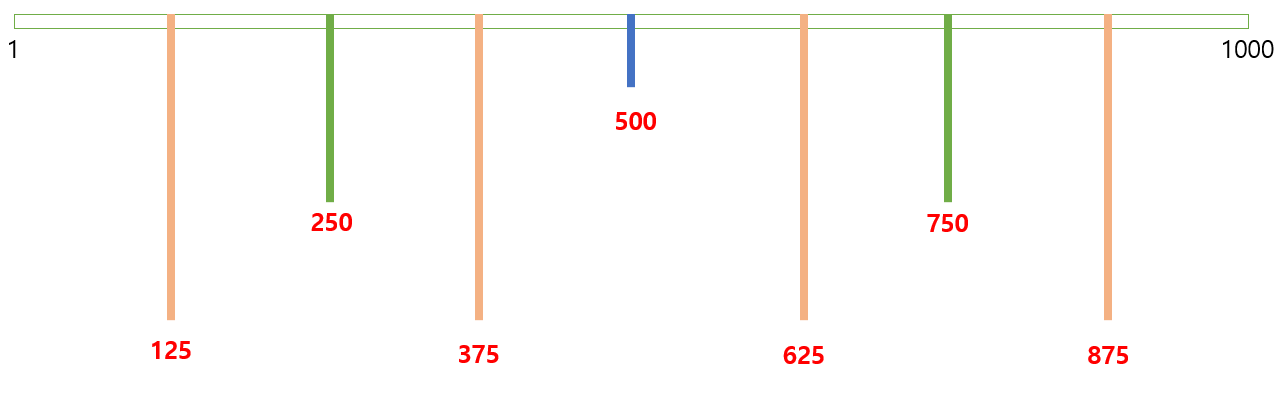
맨 처음에 500을 고르면, A가 고른 숫자가 1~499 구간에 속하는지 501~1000 구간에 속하는지 알 수 있다. 즉, 가능성을 절반으로 좁힐 수 있다.
그 다음 250 또는 750을 고르면 A가 고른 숫자는 249개 숫자중 하나가 된다.
그 다음은 125, 375, 625, 875를 고르면 A가 고른 숫자는 124개중 하나가 된다.
이런식으로 한 번에 가능성을 절반씩 날리면, 열 번이면 가능성이 1/1024가 되어 무조건 맞추게 된다.
이런 방식으로 맞춰나가는 걸 이분법(Bisection method)이라고 한다.
한 눈에 봐도 아까의 방법보다 훨씬 효율적이다. A의 숫자가 800이라고 치면, 아까의 근사법으로 접근했다면 계산이 800번 필요하지만, 이분법으로 접근하면 열 번이면 된다. 그나마 1~1000이니까 이정도지, 1~백만이었으면 차이는 훨씬 더 했을 것이다.
아까의 세 제곱근 구하기 문제에 이분법을 적용시켜보자.
저점을 Low, 고점을 High라는 변수로 지정한다.
세제곱근은 0~입력값 사이에 있을테니, Low = 0, High = 입력값으로 설정한다.
1. Low와 High의 평균 = guess, guess의 세 제곱과 입력값을 비교한다.
A - 원하는 오차범위 이내라면 출력.
B - 만약 세제곱한 값이 입력값보다 크다면, 우리가 원하는 값은 현재 guess 값보다 작다. 따라서 High = guess로 바꾼 다음 1을 반복.
C - 만약 세제곱한 값이 입력값보다 작다면, 우리가 원하는 값은 현재 guess 값보다 크다. 따라서 Low = guess로 바꾼 다음 1을 반복.
cube = int(input ("숫자를 입력해주세요."))
epsilon = 0.01 #허용 오차
guess = 0 #예측값
num_guess = 0 #예측횟수
low = 0
high = cube
guess = cube/2
while abs(guess**3-cube) >= epsilon : #abs()는 절댓값을 반환하는 함수이다.
if (guess**3 < cube) :
low = guess
else :
high = guess
guess = (high+low)/2.0 #다음번 guess는 high와 low의 평균
num_guess+=1
print ("세 제곱근은",guess,"입니다. 총",num_guess,"회 예측하였습니다.")
예측 횟수가 획기적으로 줄어든 것을 확인할 수 있다.
epsilon을 엄청 작게 하고 cube 값을 크게 해도 잘 버틴다.
결과가 같아도 어떤 알고리즘을 쓰느냐에 따라 속도가 천차만별이다.
Challenge > 사실 이 프로그램에는 맹점이 있다.
1. 절댓값이 1보다 작은 숫자의 경우, 세제곱근이 입력값보다 크기 때문에 이 방식으로 구해지지 않는다.
해결법 -> 절댓값이 1보다 작은 숫자를 입력할 시 입력값~1의 범위에서 guess 하도록 바꾸기
2. 음수의 경우에도 이 방식으로 구해지지 않는다.
해결법 -> 음수를 입력하면 (-1)을 곱해서 세제곱근을 구한 다음 다시 (-1)을 곱하기
코딩은 셀프.
'MIT challenge > 6.0001 - 파이썬을 통한 컴퓨터과학 입문' 카테고리의 다른 글
| 4강 - Decomposition, Abstraction, and Functions (0) | 2023.01.13 |
|---|---|
| 3강 In-class Questions (0) | 2022.11.26 |
| 1, 2강 In-class Questions (0) | 2022.11.25 |
| 2강 - Branching and Iteration (0) | 2022.11.24 |
| 1강 - What is computation? (0) | 2022.11.22 |



